性的（無）関係の(非）論理
小生が1990年代、某出版社から委嘱され、主にセミネール『アンコール』の読解 として原稿用紙に200枚弱書いたものです。《
2. 性的(無)関係の(非)論理》の全文と《5. ラカンとアリストテレス[1] 》の冒頭部分のみを載せました。
・1.象徴界から現実界へ
・2. 性的（無）関係の（非）論理
・3.極限としての女性
・4.主人の言説とヒステリー者の言説
・5 ラカンとアリストテレス[1]
・6.ラカンとアリストテレス[2]
・7.バロック
・8.結語
｢アンコール｣第7講、の冒頭で、性差の論理は、まず、量記号を用いた4つの命題式によってしめされる。
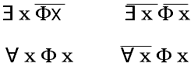
とりあえず、ラカン自身の説明を聞いてみよう。
言葉を話す人間であるならば、だれでもこれら左右のどちらかの側に記入されます。左下の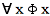
は次のことを示しています。すなわち、男根の機能によって、「すべて」としての男性は記入されます。ただしこの機能には限界があります。それは
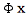の機能が否定されるひとつのｘの存在、つまり
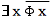によってです。父親の機能と呼ばれているものがそれです。この機能によって否定が付されて
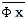といった命題が成立します。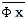は去勢によって、いかなる方法によっても書き込まれることのない性的関係を補足するsuppléerものの活動を支えるのです。「すべて」はそれゆえ、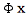を全面
的に否定するものである項として定められた例外にもとづいているのです。
反対側には語る人間の女性の側の記入がみられます。語る人間はだれでも、フロイト理論はっきり述べられているように、そのひとが男性の属性を有していようといまいと――この属性についても定義づけしなくてはならないでしょうが――この部位
に記入されることが許されます。そこに記入されると、そのひとは、いかなる普遍性をももつことができません。すべてではないpas
toutものとなります。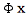に自己を位
置づけるかそうしないかといった選択権を与えられるかぎりそうなのです。
ラカンの4つの式は、伝統的論理学の4つの命題、全称肯定命題（Ａ）、全称否定命題（Ｅ）、特殊肯定命題（Ｉ）、特殊否定命題（Ｏ）のそれぞれに対応するものである。
しかしながらラカンは伝統論理学に修正を施しているのであって、それがかれ独自の表記の仕方として表されているのである。
両者を比較してみよう。
1) 伝統的論理学の関数fonctionを示すｆはラカンにおいてはファルスをしめすΦに置き換えられて
いる。
２)〔2〕と〔6〕、〔4〕と〔8〕との間には否定を表す―の記号の付され方がことなっている。
１) については次のような説明がなされよう。
フロイトの『ト－テムとタブ－』における原父は、去勢をまぬかれた唯一の男子である（
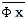
）．この原父の
存在により、かれ以外のすべてのの男子は去勢を受ける（
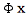
）。去勢の法が効力を持つためには、
いいかえればこの法が普遍的であるためにはこの法のがえ外部にあって、この法をまぬ
かえているある存在が必要となるのである。 こうして男性の側の２つの式
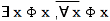
が導き出される。
否定の記号の付され方は、ここでは、伝統的論理学の場合と同様である。
ついで２）についてであるが、普遍命題
注）に否定がふされる場合、それは法のカテゴリ－に対してでなければならない。
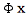
においてΦはファルスの法、ｘはその法が適用される主体であるが、否定は法に対してでなく、
法の普遍性に対して付されるべきである。すなわち
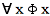
である。これは、「ファルスの法が普遍的には効力を持ちえない主体がそんざいする」と読まれる。pas-touteとは「普遍的には……ない」のいみである。いっぽう、_の法そのものが否定される場合、その法を否定する別
の法が規定される。女性 において原父に相当するような「原母」などといったようなものは存在しない。つまり女性の側において、Φの法を否定するような法を具現するものは存在しない。こうして
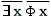
が導き出される。
注）universaireをここでは全称命題ではなく普遍命題とした。そもそも伝統的論理において「すべて」が普遍と同一視されるところに問題があるのである。
様態論理
伝統的命題論理において命題の意味づけはその命題の信理値のみが問題であった。たとえばＡおよびＢがともに真であれば、両者の様相が異なるものであってもＡ_Ｂという関係が成り立った。様相論理は必然、偶然、可能、不可能を区別する。
いま◇を可能、□を必然とすると次のような等値関係が成立する。
このページのTOPへ